Variational methods
Calculus of Variations, optimal design and optimal control problems and variational methods for PDE.
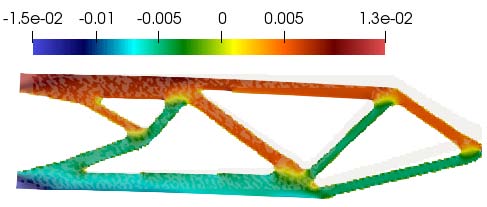
Calculus of Variations has been central in the research of the group since its beginning, particularly in the study of vector variational problems and in the development of new techniques applied in different scenarios of Solid Mechanics and Mechanical Engineering.
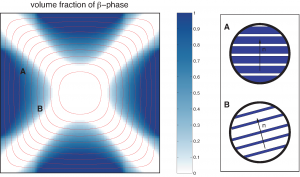
The microstructure issue is included here. This comes as a generalized solution of an ill-posed variational principle, which does not admit minimizers. From a mathematical point of view, the study of relaxation for variational problems, including the central concept of quasiconvexity, is in the core of this. From a more applied side, deepen in relaxation and the mathematical theory of microstructure bring about a better insight of several physical phenomena and engineering practical questions, such as composite materials and phase transitions.
In our research, we address the two purely mathematical problems mentioned above, from both analytical and numerical views, as well as the application of variational techniques to real-world situations from a very broad perspective.