02_2_espacios_vectoriales.nb

Práctica Segunda(Segunda parte)
ESPACIOS VECTORIALES
Trabajaremos en

1º Problema

In[1]:=

In[2]:=

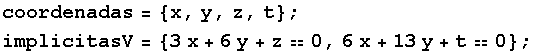
coordenadas = {x, y, z, t} ; implicitasV = {3x + 6y + z0, 6x + 13y + t0} ;

In[4]:=

Out[4]=

In[5]:=

In[6]:=

$Solve :: svars : Equations may not give solutions for all \"solve\" variables. More…$

Out[6]=

Como faltan las incognitas z y t que son parámetros un vector característico será :

In[7]:=

In[8]:=

parametros = {z, t} ; basedeV = Table[Table[Coefficient[vectorV[[j]],  &nbs ... ]

$General :: spell1 : Possible spelling error: new symbol name \"basedeV\" is similar to existing symbol \"basedeU\". More…$

Out[9]=

Un sistema de generadores del espacio U + V se halla uniendo laas dos bases anteriores

In[10]:=

Out[10]=

In[11]:=

Out[11]=

In[12]:=

Out[12]=

In[13]:=

basesuma = Table[generadorespaciosuma[[i]], {i, 3}] ; MatrixForm[basesuma]

Out[14]//MatrixForm=

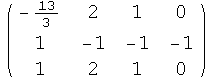
( 13 ) --- 3 2 1 0 1 -1 -1 -1 1 2 1 0

In[15]:=

param = {a, b, c} ; coordenadas = {x, y, z, t} ; parametricassuma = coordenadasTranspose[basesuma] . param

Out[17]=

In[18]:=

Out[18]=

In[19]:=

Out[19]=

RowBox[{RowBox[{RowBox[{1.2, ., -Dados}], , dos, , espacios, , vectoriales, , calcula, , su, , intersección, , U}], ⋂, , V}]

In[20]:=

param = {a, b} ; parametricasU = coordenadasTranspose[basedeU] . param

Out[21]=

In[22]:=

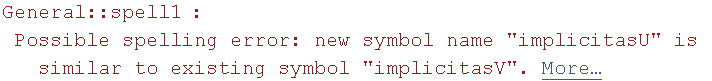
$General :: spell1 : Possible spelling error: new symbol name \"implicitasU\" is similar to existing symbol \"implicitasV\". More…$

Out[22]=

Ahora hay que formar una lista con las ecuaciones implicitas de U y de V, teniendo en cuenta que implicitasU no es un lista y habra que ponerla como tal, es decir entre llaves .

In[23]:=

interseccion = Union[{implicitasU}, implicitasV] 

Out[23]=

In[24]:=

$General :: spell1 : Possible spelling error: new symbol name \"solucion\" is similar to existing symbol \"solucionV\". More…$

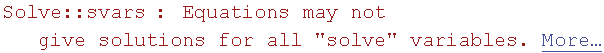
$Solve :: svars : Equations may not give solutions for all \"solve\" variables. More…$

Out[24]=

In[25]:=

Out[25]=

In[26]:=

Out[26]=

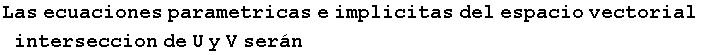
Las ecuaciones parametricas e implicitas del espacio vectorial interseccion de U y V serán

In[27]:=

parametricasUintV = coordenadasbaseinterseccion alfa Eliminate[parametricasUintV, alfa]

Out[27]=

Out[28]=

2º Problema

In[29]:=

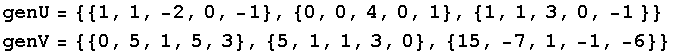
genU = {{1, 1, -2, 0, -1}, {0, 0, 4, 0, 1}, {1, 1, 3, 0, -1 }} genV = {{0, 5, 1, 5, 3}, {5, 1, 1, 3, 0}, {15, -7, 1, -1, -6}}

Out[29]=

$General :: spell1 : Possible spelling error: new symbol name \"genV\" is similar to existing symbol \"genU\". More…$

Out[30]=

In[31]:=

Out[31]=

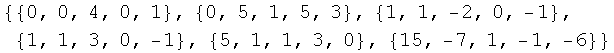
{{0, 0, 4, 0, 1}, {0, 5, 1, 5, 3}, {1, 1, -2, 0, -1}, {1, 1, 3, 0, -1}, {5, 1, 1, 3, 0}, {15, -7, 1, -1, -6}}

In[32]:=

Out[32]=

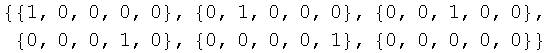
{{1, 0, 0, 0, 0}, {0, 1, 0, 0, 0}, {0, 0, 1, 0, 0}, {0, 0, 0, 1, 0}, {0, 0, 0, 0, 1}, {0, 0, 0, 0, 0}}

In[33]:=

basegenSuma = Table[genSuma[[i]], {i, 5}] ; MatrixForm[basegenSuma]

Out[34]//MatrixForm=

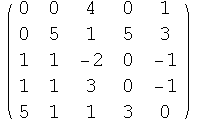
( 0 0 4 0 1 ) 0 5 1 5 3 1 1 -2 0 -1 1 1 3 0 -1 5 1 1 3 0

In[35]:=

Out[35]=

In[36]:=

parametros = {a, b, c, d, e} ; coordenadas = {x, y, z, t, u} ; paramSuma = coordenadasTranspose[basegenSuma] . parametros

Out[38]=

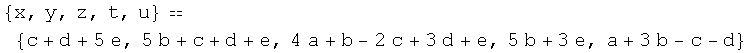
{x, y, z, t, u}  {c + d + 5 e, 5 b + c + d + e, 4 a + b - 2 c + 3 d + e, 5 b + 3 e, a + 3 b - c - d}

In[39]:=

Out[39]=

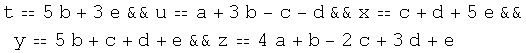
t5 b + 3 e&&ua + 3 b - c - d&&xc + d + 5 e&&y5 b + c + d + e&&z4 a + b - 2 c + 3 d + e

In[40]:=

Out[40]=

Quiere esto decir que entre las coordenadas del vector x, y, z, t, u no tiene que existir ning ... na relacion para que esté en el espacio vectorial suma, por lo tanto la suma de U y V da todo IR^5

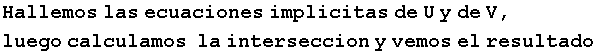
Hallemos las ecuaciones implicitas de U y de V, luego calculamos la interseccion y vemos el resultado

Parametricas de U, de V, luego las implicitas, luego su union y despues resolver

In[41]:=

parametros = {a1, a2, a3} coordenadas = {x1, x2, x3, x4, x5} parametricasdeU = coordenadasTranspose[genU] . parametros implicitasdeU = Eliminate[parametricasdeU, parametros]

Out[41]=

Out[42]=

Out[43]=

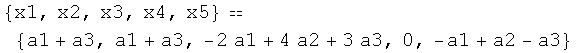
{x1, x2, x3, x4, x5}  {a1 + a3, a1 + a3, -2 a1 + 4 a2 + 3 a3, 0, -a1 + a2 - a3}

Out[44]=

In[45]:=

parametros = {a1, a2, a3} coordenadas = {x1, x2, x3, x4, x5} parametricasdeV = coordenadasTranspose[genV] . parametros implicitasdeV = Eliminate[parametricasdeV, parametros]

Out[45]=

Out[46]=

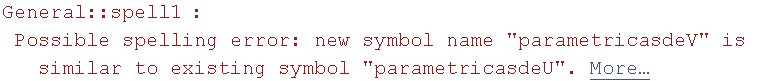
$General :: spell1 : Possible spelling error: new symbol name \"parametricasdeV\" is similar to existing symbol \"parametricasdeU\". More…$

Out[47]=

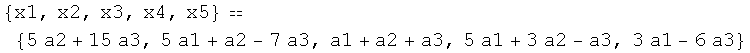
{x1, x2, x3, x4, x5}  {5 a2 + 15 a3, 5 a1 + a2 - 7 a3, a1 + a2 + a3, 5 a1 + 3 a2 - a3, 3 a1 - 6 a3}

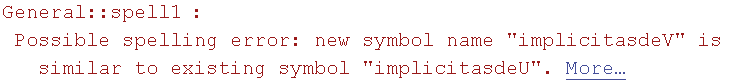
$General :: spell1 : Possible spelling error: new symbol name \"implicitasdeV\" is similar to existing symbol \"implicitasdeU\". More…$

Out[48]=

In[49]:=

sistema = Union[implicitasdeU, implicitasdeV] ; solucion = Solve[sistema, {x1, x2, x3, x4, x5}]

Out[50]=

Como la intersección es el vector nulo, concluimos que R^5 es suma directa de U y de V

3º Problema

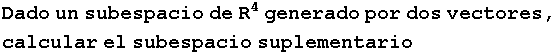
Dado un subespacio de R^4 generado por dos vectores, calcular el subespacio suplementario

In[51]:=

In[52]:=

Out[52]=

$Luego el rango es dos, bastará añadir dos vectores que sean los dela baase canónica, por ejemplo {0, 0, 0, 1} y {0, 0, 1, 0} para formar una base de R^4$